Compared: Bayesian Hierarchical vs Non-Hierarchical Modeling
Bayesian statistics is a quantitative approach that helps us deal with uncertainty. It combines our existing knowledge (prior knowledge) with new data that we observe in order to make educated guesses about unknown things. Instead of giving us a single answer, Bayesian statistics gives us a range of possibilities and their probabilities based on the information we have. This framework allows us to update our results as we gather more data and make more accurate predictions.
We start with some initial beliefs about the unknowns, and as we gather data, we update those beliefs to get a new and improved understanding of the unknowns. The result is a probability distribution called the posterior distribution, which represents our updated knowledge about the unknowns.
Bayesian Models: Background
Bayesian models have a rich historical background that traces back to the 18th century to notable contributors such as Thomas Bayes and Pierre-Simon Laplace. Thomas Bayes, an English mathematician, introduced the concept of conditional probability and developed the foundational theorem that bears his name, known as Bayes' theorem. Later, Pierre-Simon Laplace expanded upon Bayes' work and made significant contributions to the field of probability theory, including the development of Bayesian inference.
Often Bayesian models are compared to frequentist models due to their similar applications. One fundamental difference between Bayesian and frequentist approaches lies in their treatment of uncertainty. While frequentist statistics focuses on a sample of parameters and the repeated long-run behavior of estimators, Bayesian statistics takes a more subjective approach in which data is considered fixed and observed, whereas the parameters of the model are treated as random variables. Bayesian models allow for the incorporation of prior beliefs and update them based on observed data using Bayes' theorem. This incorporation of prior knowledge is a distinguishing feature of Bayesian statistics, enabling a more comprehensive and intuitive understanding of uncertainty.
The applications of Bayesian models span various fields, including machine learning, decision-making, and data analysis. In machine learning, Bayesian models are employed for tasks such as classification, regression, and clustering, providing a principled framework for probabilistic modeling. Bayesian decision theory enables optimal decision-making by integrating prior beliefs, observed data, and the costs or utilities associated with different actions. Furthermore, Bayesian models are widely used in data analysis to estimate parameters, predict future outcomes, and assess uncertainty in a wide range of domains, including finance, healthcare, and social sciences. The flexibility and broad applicability of Bayesian models make them a valuable tool for researchers and practitioners across diverse disciplines.
Shortly, in Bayesian models, we start with our initial beliefs represented by prior distributions, which can come from our previous knowledge or subjective opinions. Then, we use Bayes' theorem to update these beliefs by taking into account the observed data. The updated beliefs are represented by the posterior distributions, which combine both the prior knowledge and the information from the data. These priors are also used to calibrate marketing mix models.
When dealing with complex Bayesian models where we cannot calculate the posterior distribution analytically, we use methods such as Markov Chain Monte Carlo (MCMC), Maximum A Posteriori Estimation (MAP) or Automatic Dual Amortized Variational Inference (ADIVI). These techniques help us sample from the posterior distributions and estimate the values of the things we are interested in. MCMC methods make it possible to simulate from these distributions even when we don't have a simple formula.
Non-Hierarchical and Hierarchical Bayesian Models
Bayesian models can be broadly categorized into non-hierarchical and hierarchical models, each with its own characteristics and applications. This chapter aims to compare these two types of Bayesian models, highlighting their differences and discussing their use cases, benefits, and limitations.
What are hierarchies?
Hierarchies represent a structure where parameters or categories are organized in a cascading manner. For example, in sales data, we can have a hierarchy that spans from the country level to regions and further down to cities. Another common example is media hierarchy, where we have levels such as offline media, TV, radio, and TV stations. Hierarchies capture the relationship and dependencies between different levels, allowing for a deeper understanding of the data.
Another advantage of hierarchical models is their ability to estimate results for lower levels in the hierarchy, even when there is limited data available. The model leverages information from higher levels to make reasonable estimates for lower levels, bridging the information gap and providing valuable insights.
Non-Hierarchical Bayesian models
Non-hierarchical Bayesian models use Bayes' theorem to combine prior beliefs (expressed as prior distributions) with observed data to derive the posterior distribution. Prior beliefs, expressed as prior distributions, are combined with the observed data using Bayes' theorem to obtain the posterior distribution. Non-hierarchical models are simpler and more straightforward to implement, making them suitable when there is no explicit grouping or hierarchical structure in the data. They are commonly used for estimating parameters and making predictions in scenarios where the data can be considered as coming from a single homogeneous population.
To put it simply:
For example, let's say our prior belief is that TV advertising tends to be more effective across all countries compared to other marketing channels. However, as we collect data from different countries, we find that the effectiveness of TV advertising varies significantly across regions. In some countries, TV advertising shows a high impact on sales, while in others, its impact is minimal. The non-hierarchical Bayesian model allows us to estimate the varying effectiveness of TV advertising across countries, updating our beliefs based on the observed data from each country.
It is important to mention that in this context, we can have both pooled models and non-pooled models.
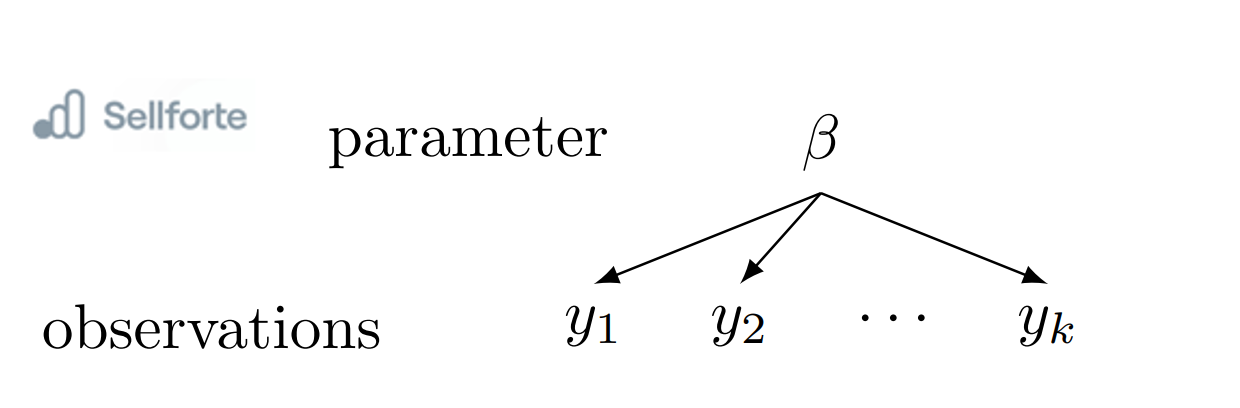
In a pooled model, we assume that the parameters for each marketing channel are the same across all countries. This means that we treat all the data as coming from a single group and estimate a common distribution for the effectiveness of each marketing channel.
 Non-Hierarchical Pooled Model
Non-Hierarchical Pooled Model
On the other hand, in a non-pooled model, we estimate separate distributions for each marketing channel in each country, allowing for variations in the effectiveness of the channels across different regions. The choice between pooled and non-pooled models depends on the underlying assumptions and the research question at hand.
 Non-Hierarchical Unpooled Model
Non-Hierarchical Unpooled Model
Non-hierarchical Bayesian models can be applied in various fields and scenarios, essentially anywhere Bayesian models are applicable.
One of the benefits of non-hierarchical models is their simplicity and ease of implementation. Non-hierarchical models are widely applicable and can be used in various fields where Bayesian models are appropriate. They provide accurate estimates when the data can be considered as coming from a single population and are useful for aggregate-level analysis or when there is no explicit grouping or hierarchy in the data.
However, a potential limitation of non-hierarchical models arises when the data exhibits hierarchical structures or iscollected from different groups. In such cases, using a non-hierarchical model ignores the hierarchical nature of the data and fails to take advantage of the group-specific information. Consequently, the estimates obtained may be less accurate compared to hierarchical models, as they do not fully incorporate all the available information.
Overall, non-hierarchical Bayesian models provide a simpler approach for analyzing data from a single group or population. They have widespread applications and offer benefits in terms of simplicity and ease of implementation. However, when hierarchical structures or group-specific information exist in the data, non-hierarchical models may lead to less accurate estimates, as they do not fully consider the hierarchical nature of the data. It is essential to carefully assess the data structure and choose the appropriate modeling approach, considering both the advantages and limitations of non-hierarchical models.
Hierarchical Bayesian Models
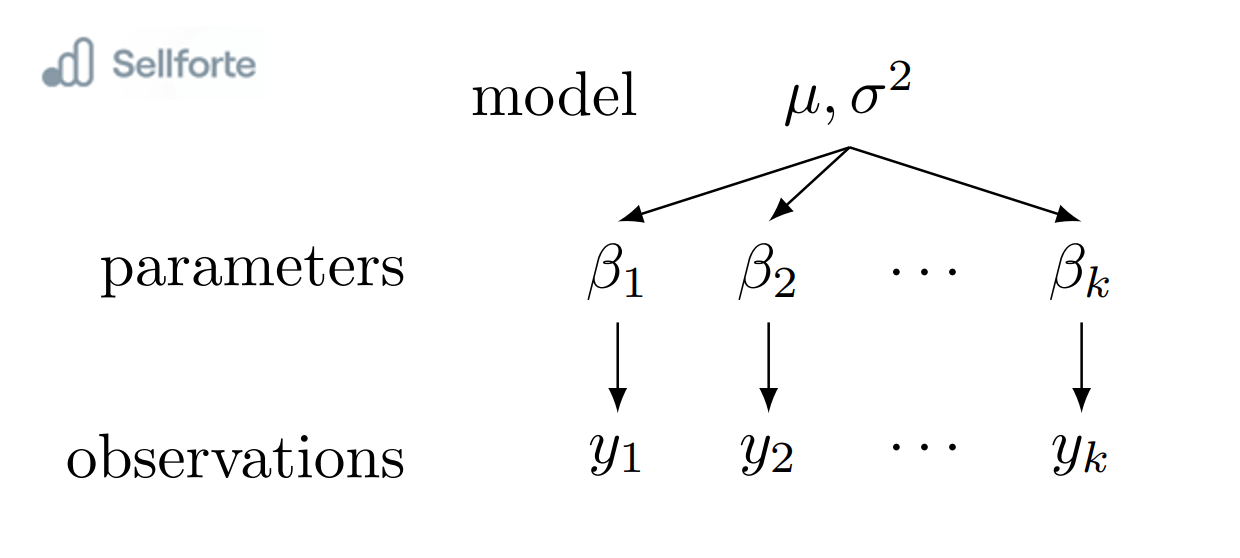
Hierarchical Bayesian models, also known as multilevel or nested models, are designed to handle data with hierarchical structures or collected from different groups. These models consider a hierarchy of parameters, where parameters at each level follow their own distributions, described by hyperparameters. The hyperparameters capture the uncertainty at a higher level and allow for sharing of information across the different levels or groups.
The main advantage of hierarchical models lies in their ability to incorporate group-level information, capturing dependencies and differences between groups. They yield more accurate estimates by considering variations between groups and including group-specific details. These models can be applied in fields like marketing, where hierarchical data structures are vital.
Let's consider the scenario where we have prior belief that TV advertising tends to be more effective across all countries compared to other marketing channels. However, as we collect data from different countries, we find that the effectiveness of TV advertising varies significantly across regions. In some countries, TV advertising shows a high impact on sales, while in others, its impact is minimal.
To address this variability and capture the dependencies across countries, we employ a hierarchical Bayesian model. This model allows us to create a hierarchy of parameters, where each country's effectiveness of TV advertising follows its own distribution, while sharing common characteristics across all countries. The hyperparameters in the hierarchical model capture the uncertainty at a higher level and enable information sharing among the countries.
 Hierarchical Model
Hierarchical Model
Hierarchical Bayesian models bring several benefits when dealing with hierarchical data:
- Incorporating hierarchical information: One of the primary advantages of hierarchical models is their ability to incorporate the hierarchical structure into the analysis. By considering the dependencies across different levels, these models provide more accurate estimates and insights.
- Marketing applications: Hierarchical models find particular utility in marketing, especially in analyzing media data. The hierarchical structure of media allows for a comprehensive assessment of the effectiveness of advertising strategies at different levels, such as analyzing the performance of TV stations within the broader TV category.
- Estimation for lower levels with limited data: Hierarchical models can estimate results for lower levels in the hierarchy, even when there is limited data available. The model leverages information from higher levels to make reasonable estimates for lower levels, bridging the information gap and providing valuable insights.
Hierarchical Bayesian models, despite their numerous benefits, present some challenges that need to be considered:
One challenge is the increased complexity in setting up these models. Implementing hierarchical Bayesian models can be costlier and more time consuming compared to non-hierarchical models. This complexity arises from the need to specify appropriate prior distributions, hyperparameters, and model structures that accurately capture the hierarchical dependencies within the data. It requires careful consideration and expertise to design the model effectively and ensure it appropriately represents the hierarchical structure. Moreover, the complexity of the models leads to more time spent on creating models and most likely also fitting the models. This means that more computational resources are spent on running the models, which leads to a higher cost.
The accuracy and reliability of the model depend on the data available at each level in the hierarchy. While hierarchical models can handle data limitations at lower levels, having sufficient data at all levels would undoubtedly lead to more precise and informative results. Moreover, when data is abundant at the lower levels, the hierarchical model can adapt and provide more detailed insights for those levels without being solely dependent on higher-level estimates. Overall, hierarchical models are flexible and can work effectively with limited data at lower levels, but having sufficient data at all levels enhances their performance and provides more accurate estimations for each level of the hierarchy.
Comparison: Non-Hierarchical vs hierarchical Bayesian models
To summarize the key differences between non-hierarchical and hierarchical Bayesian models, we present the following comparison table with additional information below:
| Difference | Non-hierarchical Bayesian Models | Hierarchical Bayesian Models |
| Structure | Assumes common distribution for all data | Incorporates hierarchical structure and group-level information |
| Implementation | Simpler and easier to implement | More complex setup. Requires more expertise |
| Applicability | Suitable when there is no explicit grouping or hierarchy | Suitable for hierarhcical data or data collected from different groups |
| Accuracy | Accurate for single population assumptions | More accurate by accounting for heterogeneity and incorporating group-specific information |
- Structure:
- Non-Hierarchical: Assumes a single common distribution for all the data, without considering any hierarchical or grouping structure.
- Hierarchical: Incorporates a hierarchical structure where parameters are drawn consecutively through different levels, allowing for capturing dependencies and heterogeneity across groups.
- Incorporation of Group-Level Information:
- Non-Hierarchical: Does not explicitly incorporate group-level information. Treats all data as if it comes from a single population.
- Hierarchical: Incorporates group-level information by assuming parameters follow a distribution at each level, capturing variations and allowing for borrowing strength across groups.
- Flexibility:
- Non-Hierarchical: Simpler and easier to implement, suitable when there is no explicit grouping or hierarchical structure.
- Hierarchical: More flexible in capturing hierarchical structures and accommodating data collected from different groups or levels.
- Accuracy:
- Non-Hierarchical: Provides accurate estimates when data can be considered as coming from a single population or when there is no need to capture group-level variations.
- Hierarchical: Allows for more accurate estimation by accounting for heterogeneity across groups and incorporating group-specific information.
Conclusion
Non-hierarchical and hierarchical Bayesian models offer distinct approaches for handling uncertainty and making inferences. Non-hierarchical models are simpler and suitable when there is no explicit grouping or hierarchy in the data. They provide accurate estimates for a single population assumption. On the other hand, hierarchical models incorporate group-level information, capture hierarchical structures, and allow for more accurate estimation by accounting for heterogeneity across groups. However, they can be more complex to set up and may require more data to achieve accurate estimations at all levels. Researchers and practitioners need to carefully consider the data structure and objectives of their analysis to select the appropriate modeling approach, taking into account the advantages and limitations of non-hierarchical and hierarchical models.
Curious to learn more? Book a demo.
You May Also Like
These Related Stories
Ultimate Buyer's Guide to MMM: How to Choose the Best Platform in 2025
What is Marketing Mix Modeling (MMM)? A Complete Guide for Marketers


